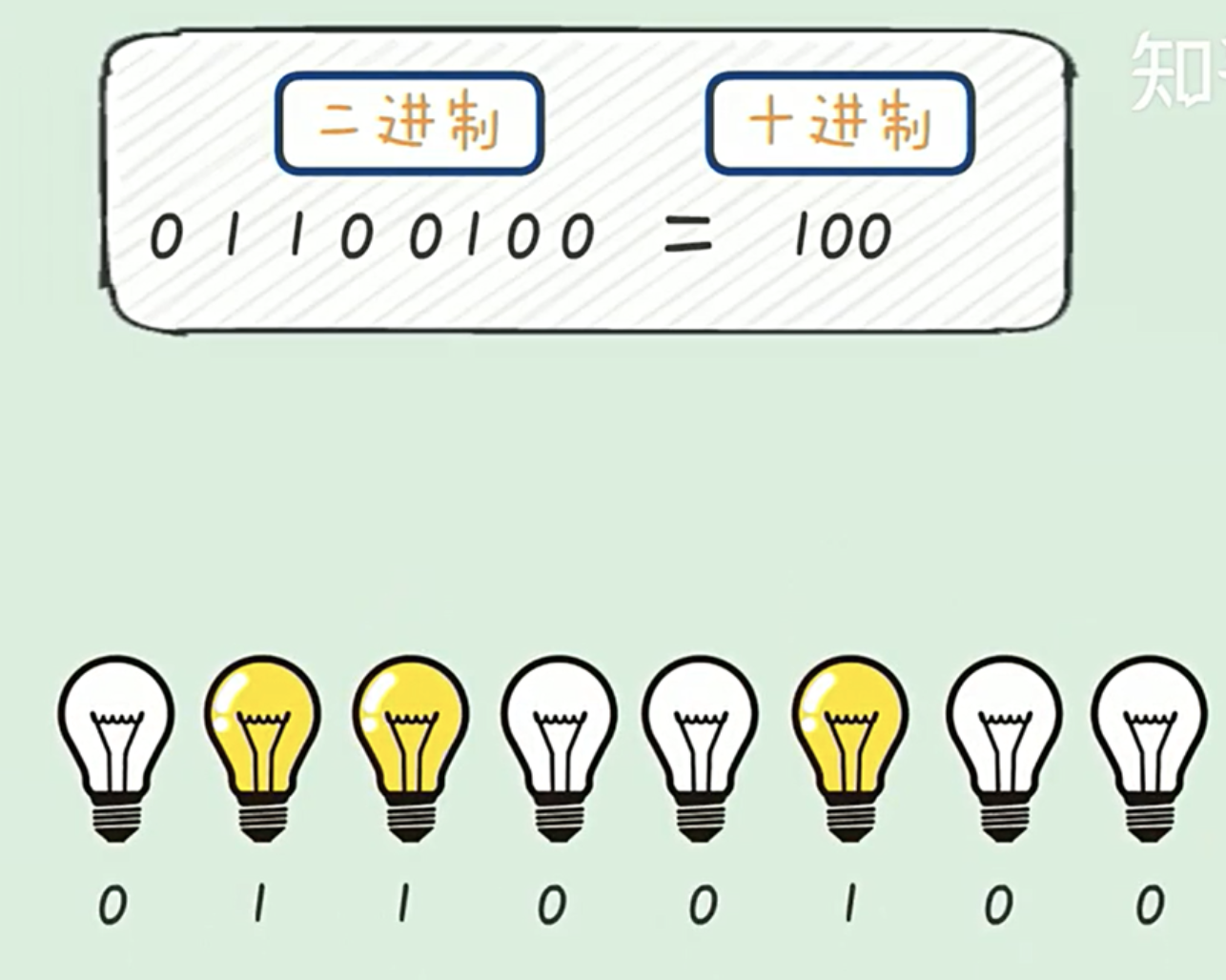
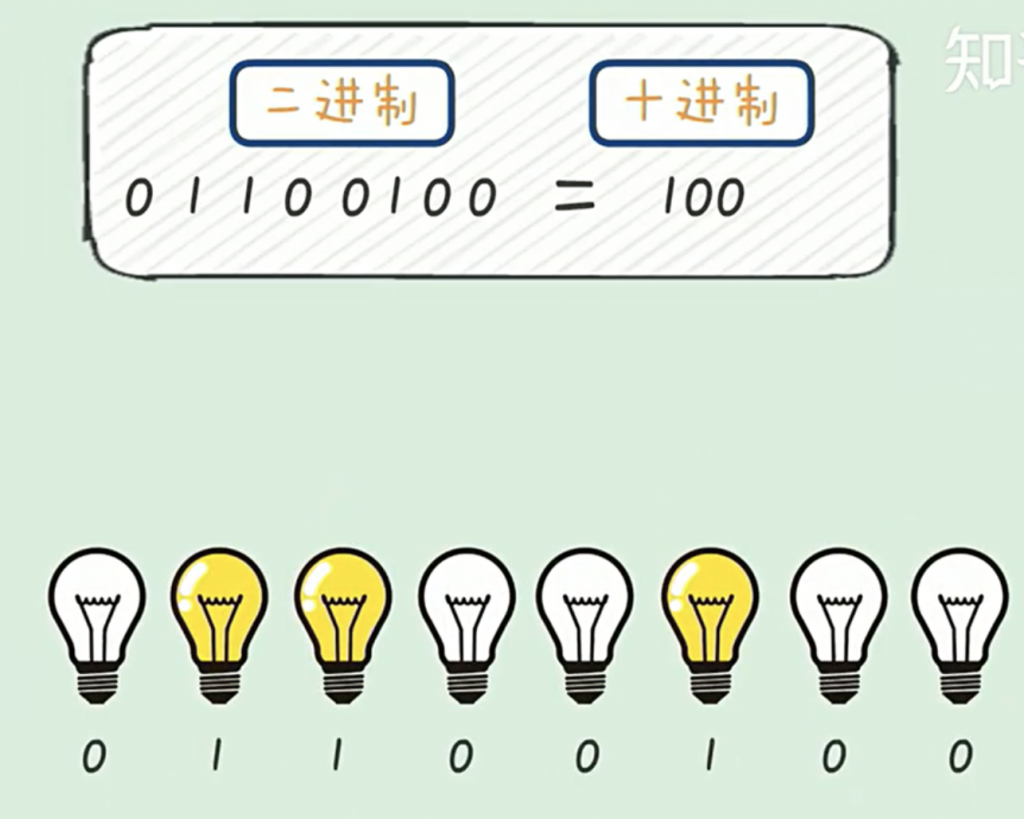
一、二进制认识
十进制有0~9,二进制只有0和1
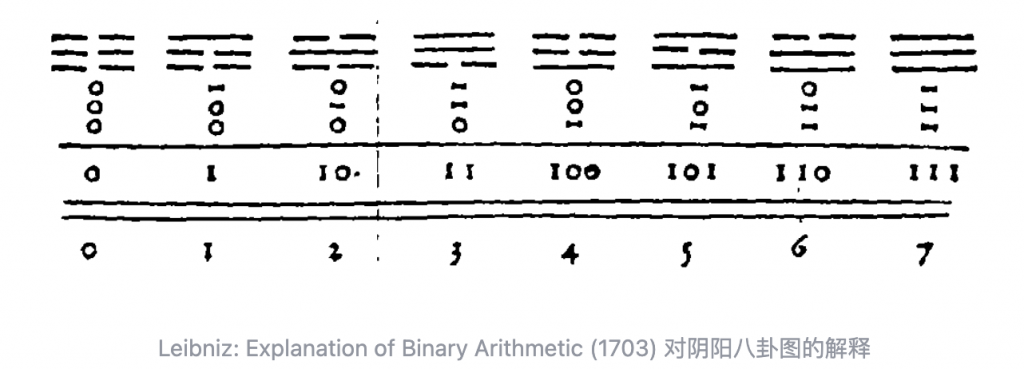
最早提出二进制的人是 17 世纪的德国数学家莱布尼茨(Gottfried Wilhelm Leibniz)。二进制还与中国传统的阴阳八卦图有关系。

伏羲是中国古典神话里的人物,是补天女娲的丈夫。传说有一天,天马载着河图从天而降,神龟背着洛书从河中浮起,伏羲看后顿悟,总结出了阴阳八卦图:

在八卦图里,使用了八个符号表示八个方向。而每个符号都是有三横组成,有的横中间断开,有的不断。如果把连续的横线视为 1,断开视为 0,那么八卦就是乾 111、坎 010、艮 100、震 001、巽 110、离 101、坤 000、兑 011,正好对应二进制的所有三位数字,转换为十进制就是 0~8 八个数字。而这正是莱布尼茨在论文里描述的内容。
二、二进制与十进制的转换
在十进制里,右边第一个数位单位为 1,往左依次为 10、100、1000… 而二进制类似,第一个数位单位同样为 1,往左则依次为 2、4、8… 下面以三位二进制数为例,转化为十进制的简单公式为:
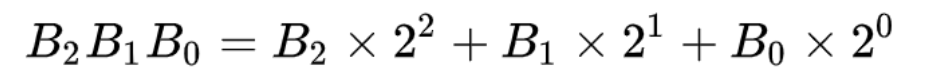
010 = 0 + 2 + 0 = 2 011 = 0 + 2 + 1 = 3 1011 = 8 + 0 + 2 + 1 = 11
十进制如何转化为二进制?




三、二进制的加减乘除
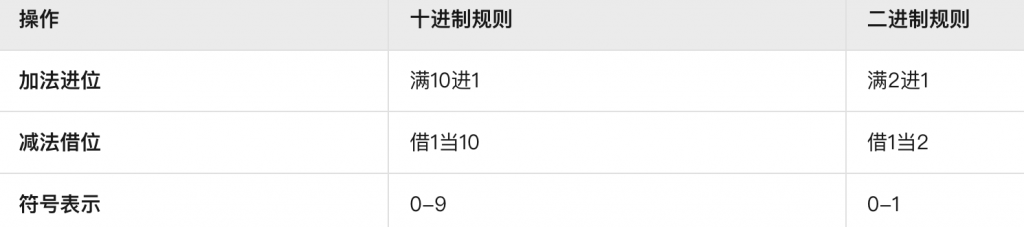
1. 二进制的加法
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10(即结果为0,进位1)
计算 1011₂ + 1101₂
2. 二进制的减法
0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 0 – 1 需要借位 → 借1当2,结果为1,前一位减1
计算 1100₂ – 1011₂
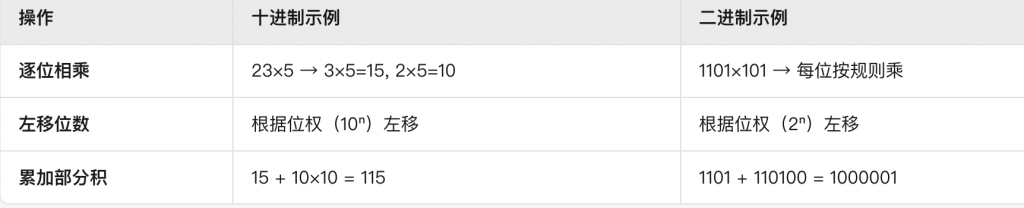
3. 二进制的乘法
逐位相乘:0 × 0 = 0 0 × 1 = 0 1 × 0 = 0 1 × 1 = 1
部分积累加:每位乘完后左移对应位数,再相加所有部分积。
计算 1101₂ × 101₂
步骤1:写出被乘数和乘数
步骤2:逐位相乘,生成部分积
乘数第1位(1) :1101 × 1 = 1101,不左移(对应2⁰位)
乘数第2位(0) :1101 × 0 = 0000,左移1位 → 00000
乘数第3位(1) :1101 × 1 = 1101,左移2位 → 110100
步骤3:将所有部分积相加
乘数为2ⁿ时的快速计算:乘数为10₂(即2),结果等于被乘数左移1位(末尾补0)。
例如:101₁₂ × 10₂ = 1010₂(5×2=10)。
4. 二进制的除法
跟十进制数一样。
计算38 ÷ 6 100110 ÷ 110
5. 对比十进制与二进制运算
四、数学问题中的应用
1. 寻找毒药瓶:
1000瓶无色无味药水,其中有1瓶毒药,服用后 1小时毒发,毒药可以无限稀释,那么1小时内,最少用多少只小白鼠能够找出毒药?
假如是8瓶药水,3只小白鼠。
000=0 001=1 010=2 011=3 100=4 101=5 110=6 111=7
每位数表示一只老鼠,0-7表示8个瓶子。 将
- 1,3,5,7号瓶子的药水混合取样给老鼠1吃;
- 2,3,6,7号瓶子的药水混合取样给老鼠2吃;
- 4,5,6,7号瓶子的药水混合取样给老鼠3吃;
死鼠相应的位标为1。 如果鼠1死了,鼠2没死,鼠3死了, 那么就是101=5号瓶子有毒。
2. 天平砝码的问题:
用天平称1~63克整数克重的物品,至少要配备几只多重的砝码(砝码只能放在天平的一端)?
没有学过二进制的人是很难想到答案的,可是如果你知道二进制数,那就不难了。我们知道二进制中只有0和1两个数字,它的各位数字的权值从小到大依次为2^0,2^1,2^2,2^3,。。。。我们用一个数的每位数字乘以其权值所得到的乘积之和来表示这个数。对于一个具有8位的二进制数来说,它可以表示的数据范围是0~2^8。
63 = 2^6 – 1 = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5
所以,我们只需配备2^0 =1,2^1 = 2,2^2 = 4,2^3 = 8,2^4 = 16,2^5 = 32六种不同克数的砝码各一个。
3. 找次品的问题:
有10箱钢珠,每个钢珠重10克。如果其中有1箱次品,次品钢珠每个重9克。请问找出这箱次品最少要称几次?
解:将10箱钢珠分别编为1~10号。
从1号箱中取1个钢珠,从2号箱中取2个钢珠……从10号箱中取10个钢珠。
共取钢珠:1+2+3+4+5+6+7+8+9+10=55(个)
将这些钢珠放到天平上称,本来应重:55×10=550(克)
如果轻了n (1≤n≤10)克,那么第几号箱就是次品。
在这个方法中,第10号箱也可不取,这样共取出45个钢珠,如果重450克,那么10号箱是次品;否则,轻几克几号箱就是次品。
五、计算机中的二进制
1. 为什么计算机中会采用二进制?
早期电子计算机(如ENIAC)尝试过十进制,但二进制在可靠性、成本和效率上全面胜出。
苏联曾研制三进制计算机(Setun),利用平衡三进制(-1, 0, 1),但未普及。
二进制是综合成本、可靠性和通用性的最优解,而非数学上的唯一选择。
1.1. 物理实现的天然适配
- 电子开关的两种状态:计算机硬件基于晶体管(开关),天然只能表示 导通(1) 和 截止(0) 两种状态。
- 抗干扰性强:区分高电平(如5V)和低电平(0V)的容错率高,即使电压轻微波动,也能清晰识别0和1。
对比十进制:若用10种电压表示10个数字,电路需精密区分微小电压差,易受噪声干扰且成本极高。
1.2. 逻辑运算的简洁性
- 布尔代数的完美映射:计算机逻辑(如与、或、非门)直接对应二进制运算。
- 运算规则简单:二进制加减乘除只需少量逻辑门即可实现,而十进制需要复杂电路。
1.3. 信息存储与传输的高效性
- 存储密度优化:二进制用最少的符号(0/1)表示信息,节省物理空间。例如:1个二进制位(bit)表示2种状态,N位可表示 2N 种信息。
- 若用三进制:1个三进制位(trit)表示3种状态,但硬件复杂度指数级上升。
- 编码扩展性强:通过组合二进制位,可表示任意复杂数据(如文字、图像、声音)。
1.4. 错误检测与纠错的便捷性
- 奇偶校验:通过增加1位校验位,快速检测数据传输中的单比特错误。
- 海明码(Hamming Code) :利用二进制位的冗余排列,自动定位并纠正错误。
1.5. 历史与技术的双重选择
- 理论奠基:乔治·布尔(George Boole)提出布尔代数(1854年),为二进制逻辑提供数学基础。
- 克劳德·香农(Claude Shannon)证明布尔代数可简化电路设计(1937年)。
- 技术演进:早期电子计算机(如ENIAC)尝试过十进制,但二进制在可靠性、成本和效率上全面胜出。
2. 布尔代数与二进制


在布尔代数上的运算被称为AND(与)、OR(或)和NOT(非)

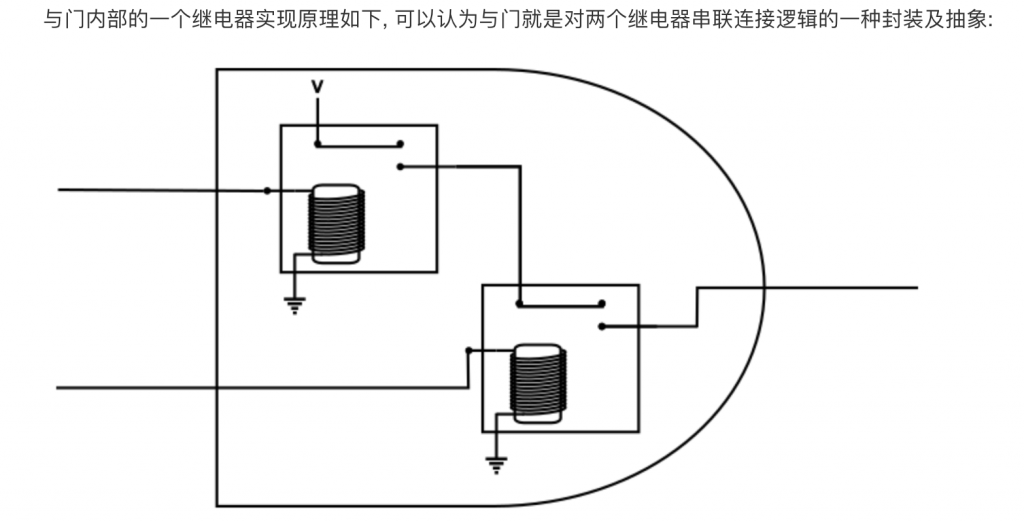
3. 计算机中的逻辑电路
3.1. 基础逻辑门
逻辑门是集成电路的基本组件,由晶体管等元件构成,通过组合高低电平信号实现二进制(1和0)的逻辑运算。例如,计算机处理器每秒执行数十亿次逻辑门操作以处理数据。
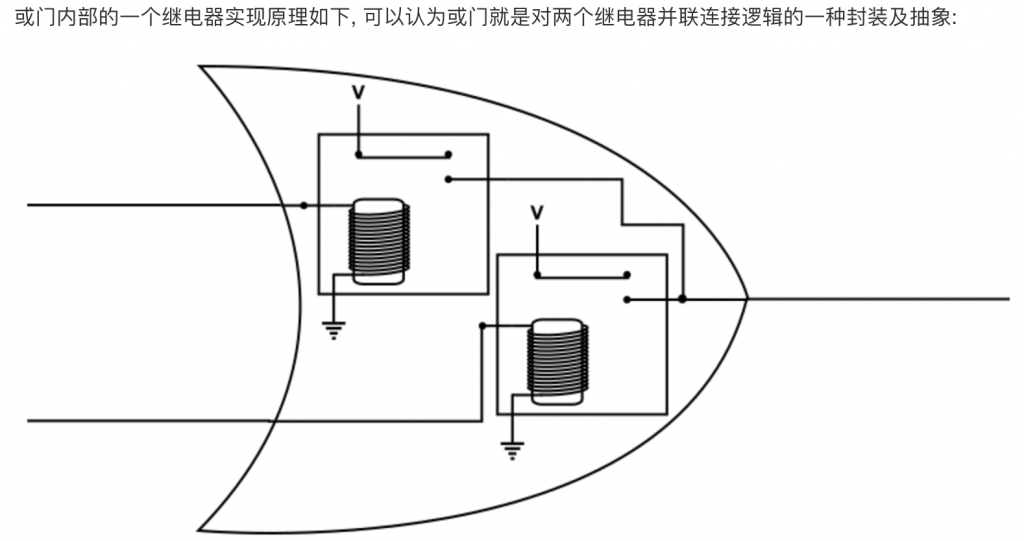
基础逻辑门:与门,或门,非门。
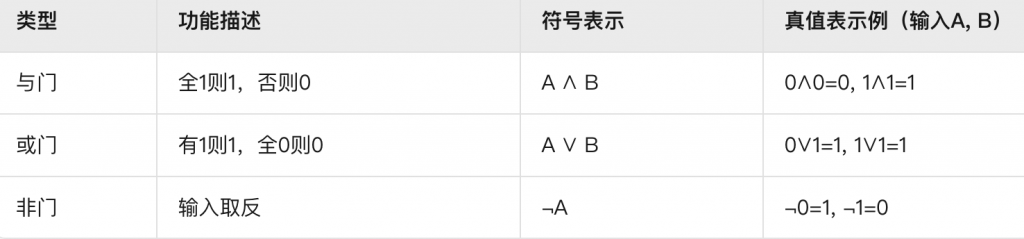
与门:
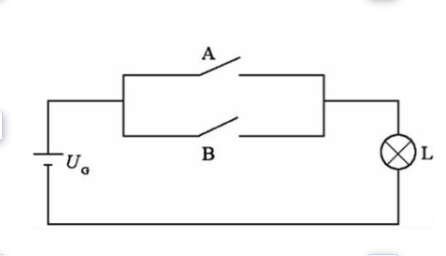
或门:
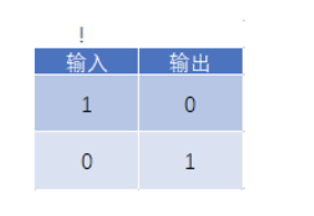
非门:
3.2. 组合逻辑门:
与非门(NAND) :与门+非门,全1则0,否则1。
或非门(NOR) :或门+非门,全0则1,否则0。
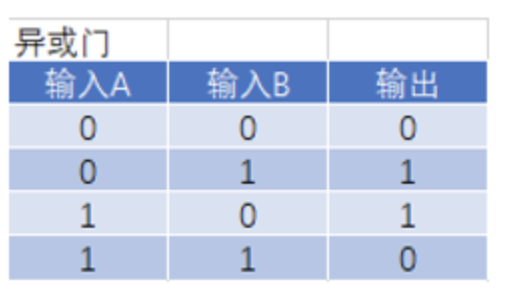
异或门(XOR) :输入不同则1,相同则0(用于加密算法)。
同或门(XNOR) :异或门的反操作,输入相同则1
异或门
异或门 也可以视作是由 两个与门 + 或门 + 非门 构成
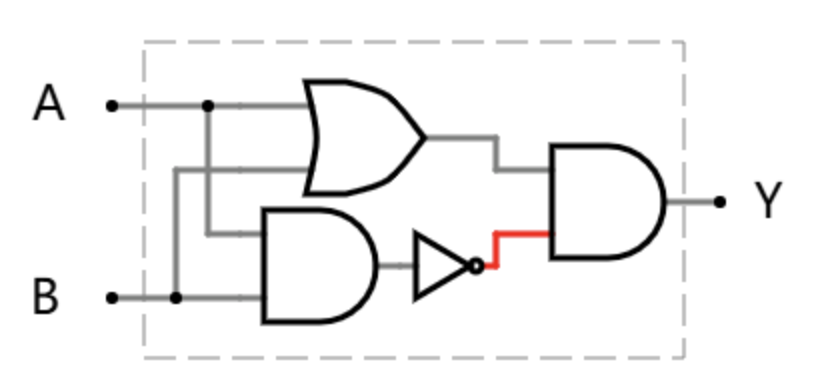
其他还有与非门,或非门,同或门就不展开描述了。
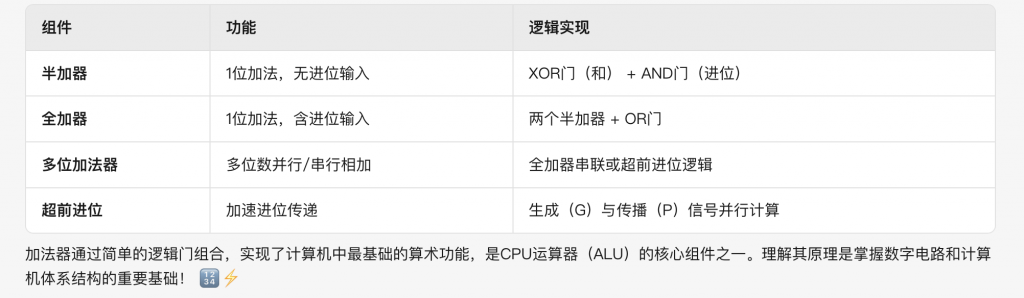
3.3. 加法器
加法器是数字电路中最基础的运算单元,用于实现二进制数的加法运算。其核心功能是通过逻辑门组合处理输入信号,输出和(Sum)与进位(Carry)。
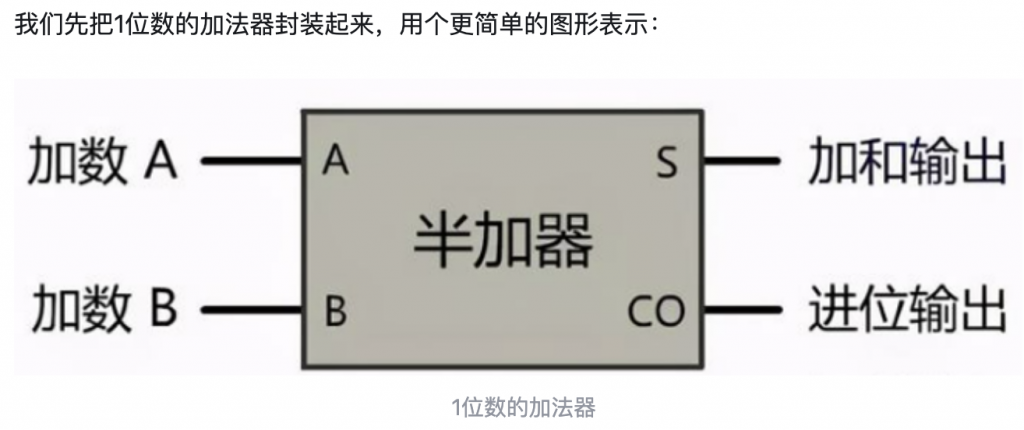
半加器(Half Adder)
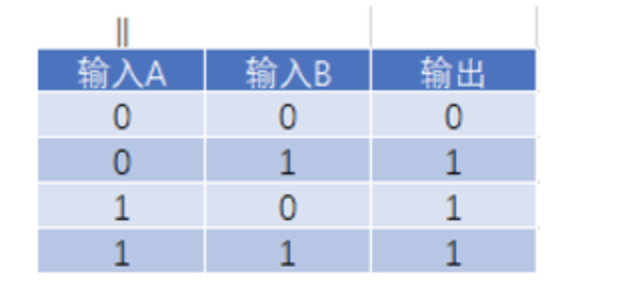
处理两个1位二进制数的相加,输入为加数A和B,输出和S(A⊕B)与进位C(A∧B)。仅适用于最低位相加,无法处理来自低位的进位。
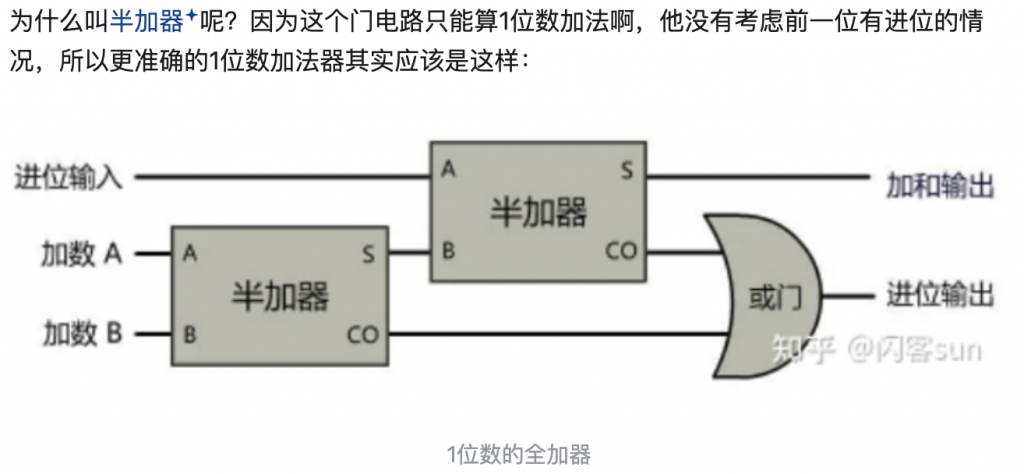
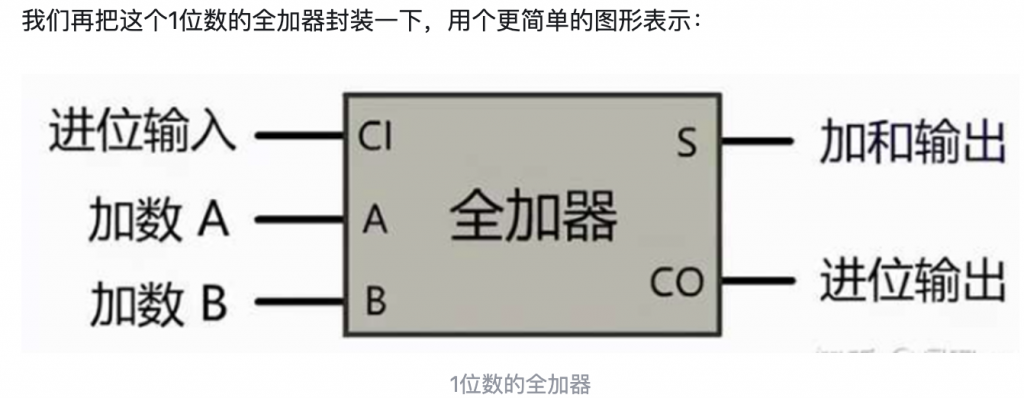
全加器(Full Adder)
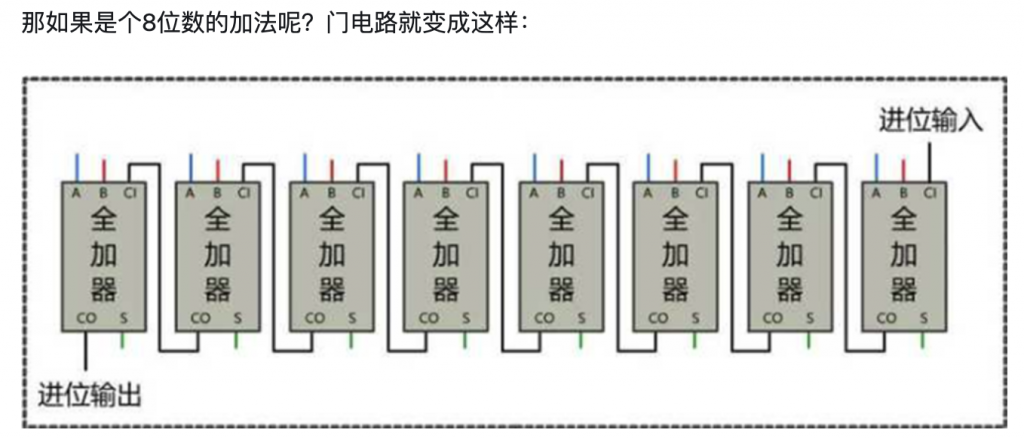
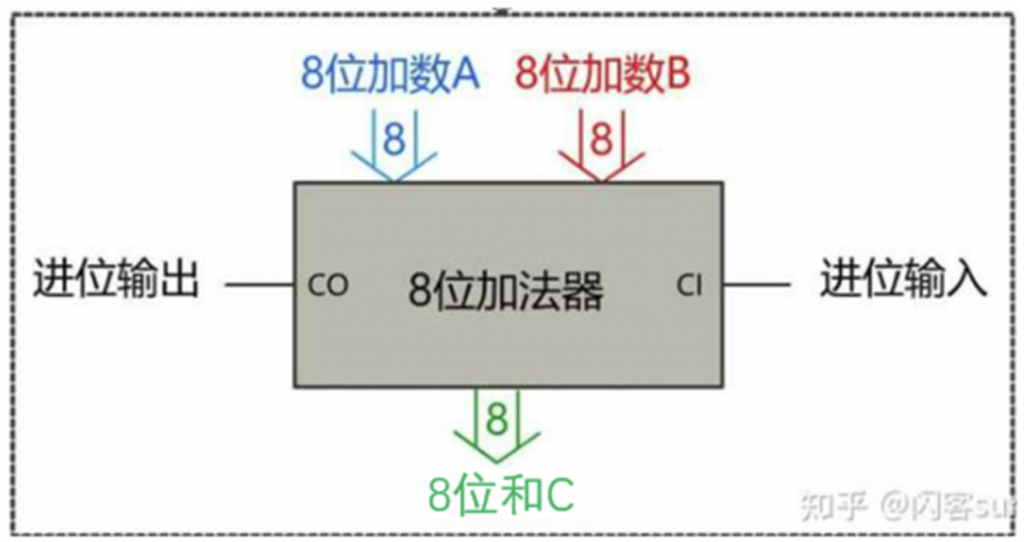
输入包括加数A、B和低位进位Cin,输出和S(A⊕B⊕Cin)与进位Cout(AB + BCin + ACin)。通过级联全加器可构建多位数加法器。
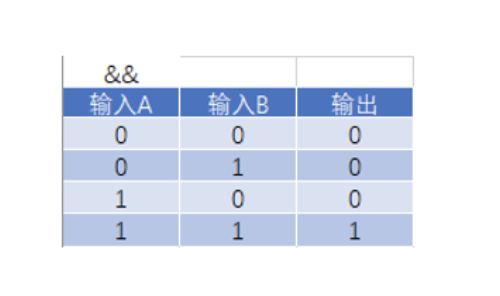
二进制加法的真值表:
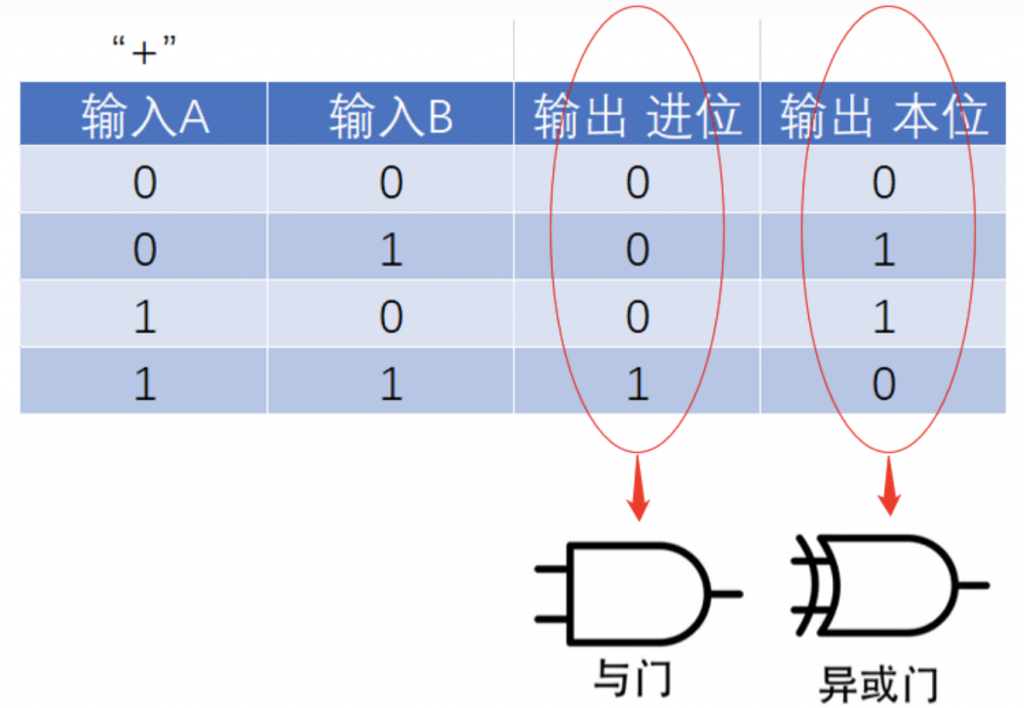
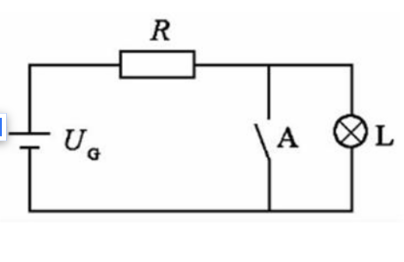
如果是1位数的加法,我们使用“与门”和“异或门”就能实现,如下图:

3.4. 课外了解
- 电子管 晶体管 二极管 三极管
- 逻辑门的电路实现
主要技术类型 TTL(晶体管-晶体管逻辑) :速度快但功耗高,早期用于74系列芯片。
CMOS(互补金属氧化物半导体) :静态功耗低、抗干扰强,广泛应用于现代集成电路(如CPU)。
MOS门电路:基于场效应管,适合大规模集成(如手机芯片)
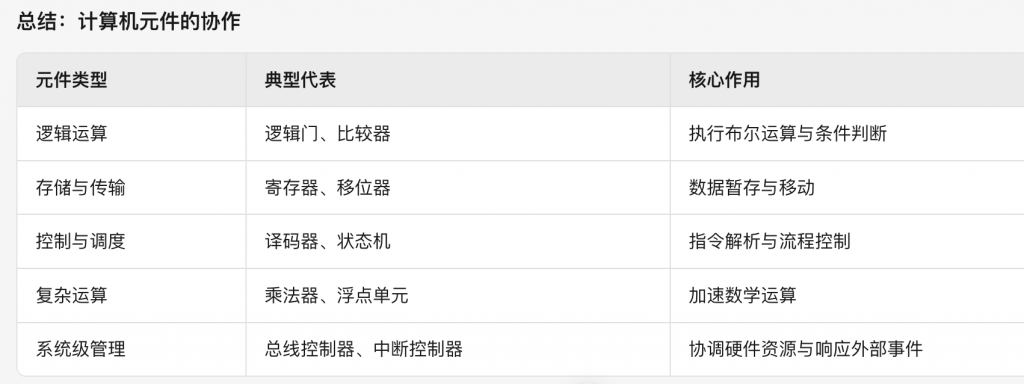
- 计算机的不同组成元件
- 逻辑门电路模拟实验
实体电路实验可以购买数字实验电路包。